Math Refresher
If you are rusty on the math concepts you learned in high school algebra and geometry, this page will highlight some of the key items we expect you are familiar with coming into TAC 380.
Table of Contents
(Supplemental) Additional Resources
If you feel like you don’t understand the examples or don’t remember learning the concepts listed in this refresher, it may be helpful to go through some Khan Academy courses.
However, we suggest first going through the rest of this refresher and only come back to these Khan Academy courses if you find yourself confused or want a more in-depth review:
Solving Quadratics
Recall that a quadratic equation is a second-degree polynomial equation of the form:
\[ax^2+bx+c=0\]With Factoring
If you’re solving a quadratic equation on paper, in some cases it may be simpler to factor the quadratic in order to solve it. For example, this equation:
\[x^2+8x+15=0\]Can be factored into:
\[(x+3)(x+5)=0\]Once you have the factors, you can solve both terms to get the solution:
\[\begin{align} x =& -3\\ x =& -5 \end{align}\]However, the downside of this approach is it requires actually factoring the equation. Although some equations are easy to factor on paper, writing code to factor an equation is not straightforward, even for equations which are easy on paper. And there are many equations which will have non-integer solutions, which are going to be challenging even on paper. Finally, in many cases the coefficients of the quadratic are represented in terms of other variables, so there isn’t anything to factor.
Using the Quadratic Formula
Given a quadratic equation of the form:
\[ax^2+bx+c=0\]The quadratic formula can solve for \(x\):
\[x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}\]The term under the square root, called the discriminant, is important for determining the number of solutions to the quadratic equation (and whether or not those solutions are real numbers):
- If \(b^2-4ac\) is positive, it means there are two real solutions to the equation
- If \(b^2-4ac\) is zero, it means there is a single real solution to the equation
- If \(b^2-4ac\) is negative, it means there are two solutions but they are imaginary
Typically, when solving quadratics for various game math problems, we only care about real solutions, so a negative discriminant means we would disregard the solution.
Trigonometric Functions
Recall that a right triangle looks like this:
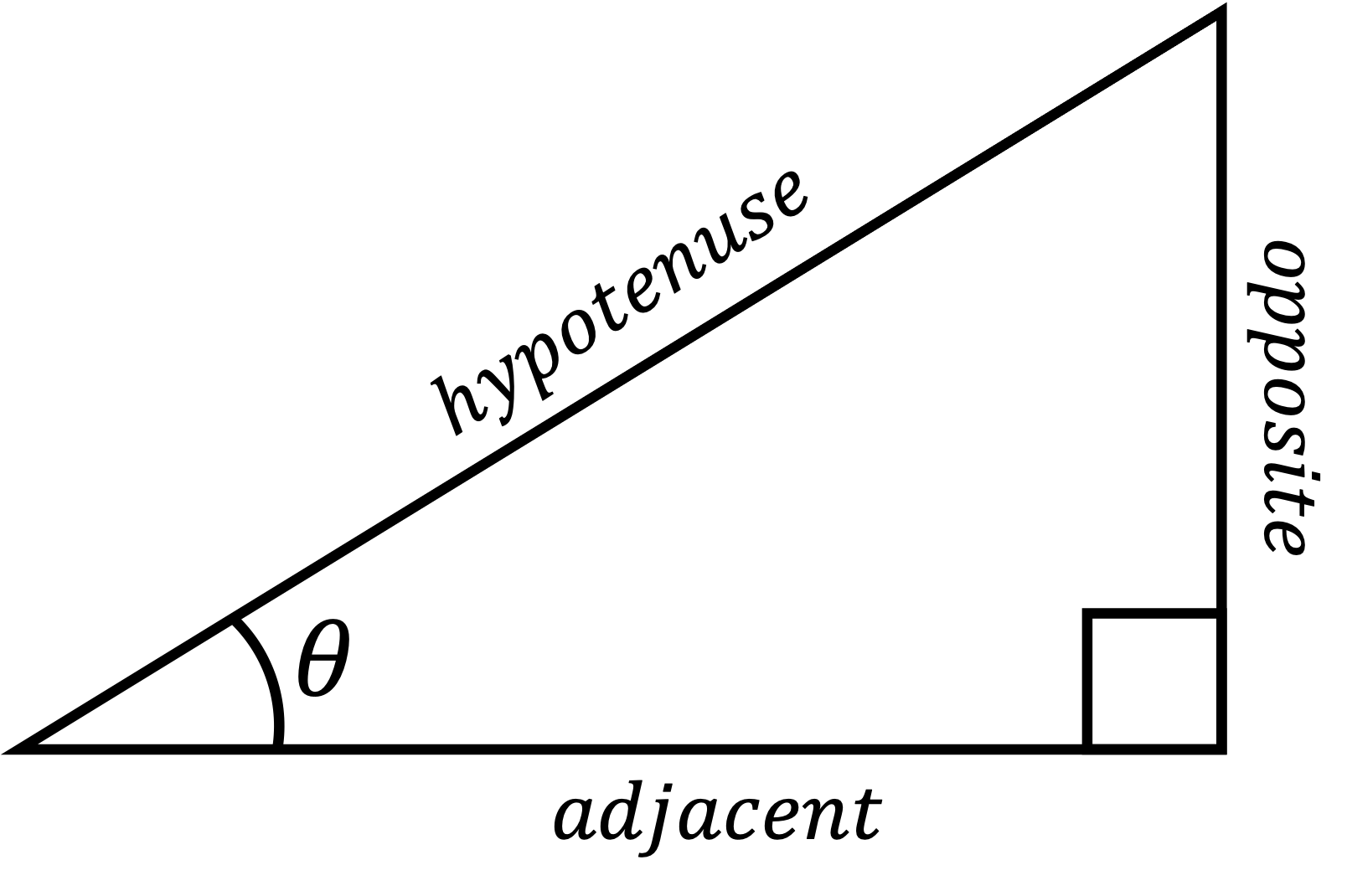
Given an angle \(\theta\), the trigonometric functions define the ratios between the length of the different sides of the triangle for that angle:
\[\begin{align} \sin \theta = & \frac{opposite}{hypotenuse} \\ \cos \theta = & \frac{adjacent}{hypotenuse} \\ \tan \theta = & \frac{opposite}{adjacent} \end{align}\]A mnemonic to help remember these equations is “SOH CAH TOA,” which breaks down to:
- Sine is Opposite over Hypotenuse
- Cosine is Adjacent over Hypotenuse
- Tangent is Opposite of Adjacent
Most commonly, you can use the trigonometric functions to solve for the length of the sides of the right triangle when you know only the angle and length one of the other sides.
For example, if we know the angle \(\theta\) and the length of the hypotenuse, we can solve for both the opposite and adjacent sides:
\[\begin{align} opposite = & hypotenuse \cos \theta \\ adjacent = & hypotenuse \sin \theta \\ \end{align}\]Of course, once you know the length of two sides of a right triangle, you can also use the Pythagorean theorem to solve for the length of the third size:
\[c^2=a^2+b^2\]where \(c\) is the length of the hypotenuse and \(a\) and \(b\) is the length of the two other sides.
Inverse Trigonometric Functions
The inverse trigonometric functions let you work in the opposite direction: given the ratio between the sides of the right triangle, you can calculate the angle \(\theta\).
For example, the inverse cosine function calculates \(\theta\) given the length of the adjacent and hypotenuse sides:
\[\theta = \cos^{-1}\frac{adjacent}{hypotenuse}\]In addition to using \(\cos^{-1}\) to represent the inverse function, there are a couple of other equivalent ways to write it as:
\[\begin{align} \theta = & \arccos\frac{adjacent}{hypotenuse} \\ \theta = & \text{acos}\frac{adjacent}{hypotenuse} \end{align}\]Using \(\text{acos}\) for arccosine is particularly relevant because that’s the naming convention used by the C++ math library. For example, the provided math library in TAC 380 uses Math::Acos for the inverse cosine function.
Law of Cosines
The law of cosines generalizes the Pythagorean theorem for non-right triangles. Given the following triangle:
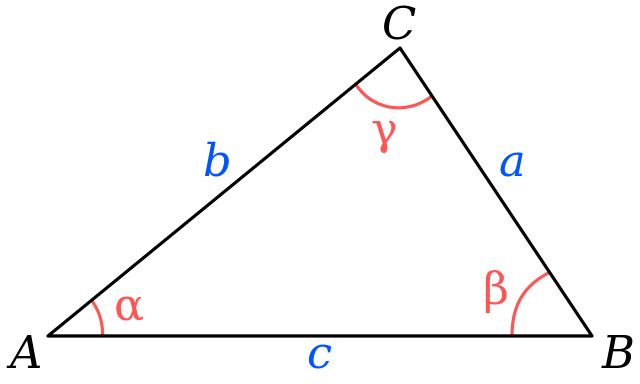
The law of cosines states that:
\[c^2 = a^2 + b^2 - 2 a b \cos\gamma\]The law of cosines can be proved in a few different ways (see), but writing proofs is beyond the scope of what you need to know for the course.
The law of cosines itself is not used very commonly by itself in games, but it is the underpinning for arguably the most important property of the dot product you will learn this semester.
Radians vs. Degrees
The trigonometric and inverse trigonometric functions have corresponding functions in the C++ math library, and the Math.h header in your starting code has wrappers for those such as Math::Cos or Math::Acos.
As in most programming languages, the assumption for these functions it that angles are always expressed in radians, so for example Math::Cos(180.0f) does not yield a particularly meaningful result, but Math::Cos(Math::Pi) does.
The library defines a few constants in the Math namespace for common radians values:
const float Pi = 3.1415926535f;
const float TwoPi = Pi * 2.0f;
const float PiOver2 = Pi / 2.0f;
These correspond to the angles 180°, 360°, and 90°.
To help with conversion between radians and degrees, we also provide a Math::ToRadians function, so you can write:
Math::Cos(Math::ToRadians(180.0f))
Unit Circle
The unit circle is a circle with a unit radius centered about the origin:

Every \((x,y)\) point on the unit circle satisfies the equation:
\[x^2 + y^2 = 1\]Another way to look at the unit circle is that \(|x|\) and \(|y|\) are the lengths of the sides of a right triangle with a hypotenuse of length \(1\):
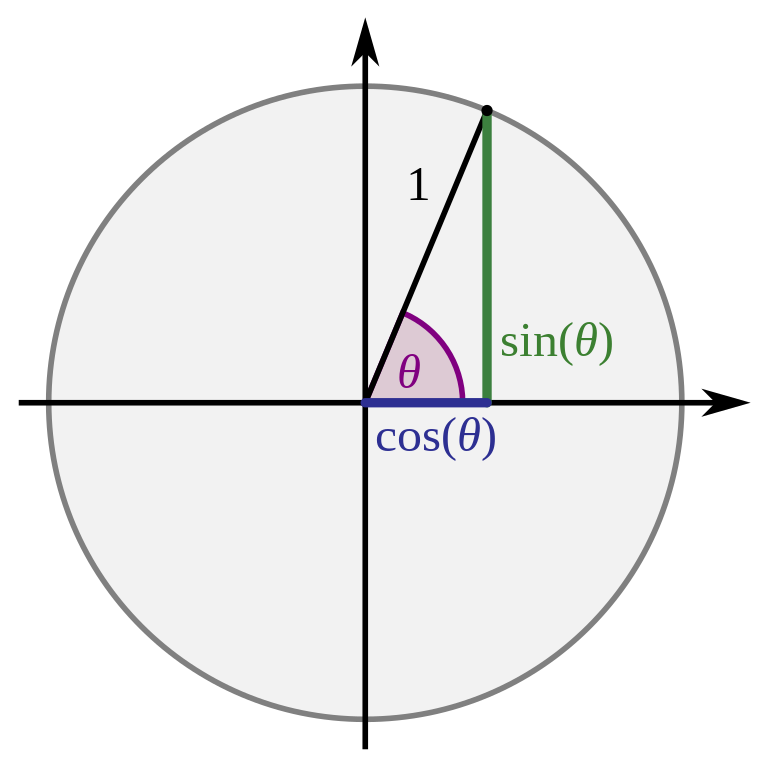
Given an angle \(\theta\) you can then calculate the \((x,y)\) point on the unit circle at that angle with:
\[\begin{align} x = & \hspace{0.15cm} \cos\theta \\ y = & \hspace{0.15cm} \sin\theta \end{align}\]Parametric Equations
This equation at the end of the preceding section is a parametric equation expresses it expresses the points on the circle in terms of another parameter (in this case, \(\theta\)).
Typically (though not required to), parametric equations use \(t\) as the name of the parameter. For example, the following parametric equation defines the \(x\) and \(y\) points for a circle of radius \(r\) offset from the origin by \((a,b)\):
\[\begin{align} x(t) = & r \cos t + a \\ y(t) = & r \sin t + b \end{align}\]In games, we use parametric equations to represent time intervals in which we want to test something. For example, if we want to test whethere two moving spheres intersect, we represent their positions as parametric equations where \(t = 0\) corresponds to the start of the time interval and \(t = 1\) corresponds to the end of the time interval.
You can use parametric equations to represent many different types of curves and surfaces. For instance, a paremetric equation can represent a line given the following:
- \(P=(x_0,y_0)\) is a point on the line
- \(\vec{v}=\langle a,b \rangle \) is the direction vector of the line
The line can be represented as:
\[\left. \begin{align} x(t) = & x_0 + at \\ y(t) = & y_0 + bt \end{align} \right\}\text{where}\hspace{0.15cm}-\infty \leq t \leq \infty\]If you haven’t learned about vectors yet, that’s okay, as we cover the basics in lecture.
Plane Equation
Recall that a plane is an infinite two-dimensional surface. The general equation of a plane is in the form of:
\[ax + by + cz + d = 0\]In this general form, \(a\), \(b\), and \(c\) are the components of the normal vector of the plane, or a unit-length vector that is perpendicular to the plane. But what’s \(d\)?
Given a point that’s on the plane \((x_0,y_0,z_0)\), you can substitute these components into the general general to solve for \(d\):
\[\begin{eqnarray} ax_0 + by_0 + cz_0 + d = 0 \\ d = -(ax_0 + by_0 + cz_0) \end{eqnarray}\]You can then resubstitute this equation for \(d\) into the general equation and factor the terms to get the “scalar form” of the plane equation:
\[\begin{eqnarray} ax + by + cz + -(ax_0 + by_0 + cz_0) = 0 \\ ax - ax_0 + by - by_0 + cz - cz_0 = 0 \\ a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 \end{eqnarray}\]You can then test whether some other arbitrary point satisfies the equation, and if it does, it means that point is on the plane.
Kinematics
Although more physics than mathematics, we use kinematics to represent the motion of objects in games.
- \(r(t)\) is the position of an object at time \(t\)
- \(v(t)\) is the velocity (change in position over time), and is the derivative of \(r(t)\)
- \(a(t)\) is the acceleration (change in velocity over time), and is the derivative of \(v(t)\)
You don’t need to know calculus for this class, as we won’t be taking symbolic derivatives or integrals. However, “under the hood,” you are doing calculus any time you update the position of an object in terms of delta time.
In terms of units, if the position is expressed in meters \(m\) then:
- Velocity is in \(m/s\)
- Acceleration is in \(m/s^2\)
In our assignments we will just say “units” instead of any specific type of measurement like meters.